Sotaro Katayama
[GitHub/Google Scolar/Research Gate]
Email: sotaro.katayama@gmail.com
I am a reseacher being interested in optimization-based control and planning of robotic systems, especially model predictive control (MPC) for legged robotics. I was a Ph. D. student in Integrated Dynamical Systems Lab (English/Japanese) advised by Prof. Toshiyuki Ohtsuka.
Education
-
Kyoto University, 2019 - Present
Ph.D student -
Graduate School of Informatics, Kyoto University, 2017 - 2019
Master of Informatics -
Kyoto University, 2013 - 2017
Bachelor of Engineering Science
Work Experience
- Sony, 2023 - Current
- OMRON SINIC X (Internship) 2021 - 2022
- Hitachi, Ltd., R&D, 2019 - 2020
Selected Research Projects
Whole-body model predictive control (MPC) via online switching time optimization (STO)
This project presents a novel whole-body MPC in which the future trajectory and switching times (contact timings) are simultaneously optimized online, which pushes the ability of the whole-body MPC.
Figure: Comparison between the proposed MPC-STO and the conventional MPC.

Paper: S. Katayama, T. Ohtsuka, “Whole-body model predictive control with rigid contacts via online switching time optimization,” 2022 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2022), arXiv preprint arXiv:2203.00997.
Lifted contact dynamics for efficient optimal control of rigid body systems with contacts
This project presents a lifting approach for optimal control of rigid body systems with contacts (e.g., legged robots). We lift the original optimization problem into a higher dimensional one to relax the high nonlinearity due to the contact dynamics while keeping the computational efficiency. Numerical results on whole-body optimal control of legged robots show that the proposed method can reduce the computational time drastically in the presence of active friction cone constraints.
Figure: CPU time comparison between the proposed (DMS-LCD) and previous methods (DMS-CD, DMS-ID, FDDP, iLQR) for whole-body optimal control of a quadrupedal robot.

Paper: S. Katayama, T. Ohtsuka, “Lifted contact dynamics for efficient optimal control of rigid body systems with contacts,” 2022 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2022), arXiv preprint arXiv:2108.01781.
Structure-exploiting Newton-type method for optimal control of switched systems
This project proposes an efficient Newton-type algorithm for solving the optimal control problems of switches systems under a given switching sequence. The proposed method achieves 1) fast local convergence (a local convergence is guaranteed), 2) fast Newton-step computation (linear time-complexity w.r.t. the horizon length). Numerical experiments demonstrate that our method can optimize the whole-body trajectory of complex robot motions in significant short times.
Figure: Convergence behavior of the proposed method for whole-body optimal control of a quadrupedal robot. t1 and t2 are the switching times.


Paper: S. Katayama, T. Ohtsuka, “Structure-exploiting Newton-type method for optimal control of switched systems,” arXiv preprint arXiv:2112.07232.
Efficient Riccati recursion for optimal control problems with pure-state equality constraints
Riccati recursion algorithm is a well-known efficient algorithm both in the MPC community and robotics community (e.g., known as DDP or iLQR). One of its drawbacks is that it cannot pure-state equality constraints efficiently, which typically arise in robotic problems. We propose an efficient constraint-transformation approach while the second-order convergence speed and certain optimality are guaranteed. The numerical results on whole-body optimal control of legged robots show the efficiency of the proposed method.
Figure: CPU time comparison between the proposed, previous, and augmented Lagrangian (AL) methods for whole-body optimal control of a quadrupedal trotting.
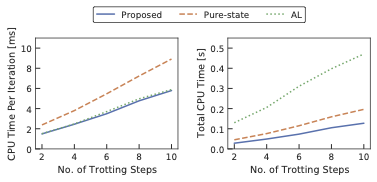
Paper: S. Katayama, T. Ohtsuka, “Efficient Riccati recursion for optimal control problems with pure-state equality constraints,” 2022 American Control Conference (ACC 2022), arXiv:2102.09731.
Efficient solution method based on inverse dynamics for optimal control problems of rigid body systems
This project presents a solution method of optimal control problem of rigid body systems leveraging inverse dynamics-based formulation, which is particularly efficient for fixed-based robots (e.g., robot manipulators).
Figure: CPU time comparison between the proposed and existing methods for optimal control of a robot manipulator.
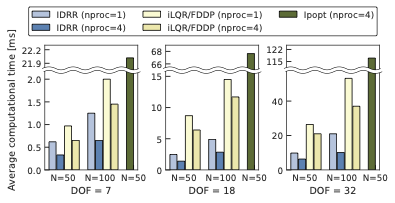
Paper: S. Katayama, T. Ohtsuka, “Efficient solution method based on inverse dynamics for optimal control problems of rigid body systems,” IEEE International Conference on Robotics and Automation 2021 (ICRA 2021), 2021 (arXiv:2106.04176).
Publications
- S. Katayama, T. Taniai, K. Tanaka, “Quasistatic contact-rich manipulation via linear complementarity quadratic programming,” 2022 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2022), arXiv preprint arXiv:2210.13908.
- S. Katayama, T. Ohtsuka, “Whole-body model predictive control with rigid contacts via online switching time optimization,” 2022 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2022), arXiv preprint arXiv:2203.00997.
- S. Katayama, T. Ohtsuka, “Structure-exploiting Newton-type method for optimal control of switched systems,” arXiv preprint arXiv:2112.07232.
- S. Katayama, T. Ohtsuka, “Lifted contact dynamics for efficient optimal control of rigid body systems with contacts,” 2022 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2022), arXiv preprint arXiv:2108.01781.
- S. Katayama, T. Ohtsuka, “Efficient Riccati recursion for optimal control problems with pure-state equality constraints,” 2022 American Control Conference (ACC 2022), arXiv:2102.09731.
- S. Katayama, T. Ohtsuka, “Inverse dynamics‐based formulation of finite horizon optimal control problems for rigid‐body system,” Optimal Control Applications and Methods, pp. 1-19, 2021, https://doi.org/10.1002/oca.2750.
- S. Katayama, T. Ohtsuka, “Riccati recursion for optimal control problems of nonlinear switched systems,” IFAC Conference on Nonlinear Model Predictive Control 2021 (NMPC 2021), 2021 (arXiv:2102.02065).
- S. Katayama, T. Ohtsuka, “Efficient solution method based on inverse dynamics for optimal control problems of rigid body systems,” IEEE International Conference on Robotics and Automation 2021 (ICRA 2021), 2021 (arXiv:2106.04176).
- S. Katayama, T. Ohtsuka, “Efficient solution method based on inverse dynamics of optimal control problems for fixed-based rigid-body systems,” IFAC World Congress 2020, Vol. 53, No. 2, pp. 6483-6489, 2020, https://doi.org/10.1016/j.ifacol.2020.12.1794.
- S. Katayama, T. Ohtsuka, “Automatic code generation tool for nonlinear model predictive control with Jupyter,” IFAC World Congress 2020, Vol. 53, No. 2, pp. 7033-7040, https://doi.org/10.1016/j.ifacol.2020.12.447.
- S. Katayama, M. Doi, T. Ohtsuka, “A moving switching sequence approach for nonlinear model predictive control of switched systems with state-dependent switches and state jumps,” International Journal of Robust and Nonlinear Control, Vol. 30, No.2, pp. 719-740, 2020, https://doi.org/10.1002/rnc.4804.
- S. Katayama and T. Ohtsuka, “Scenario-based nonlinear model predictive control for switched systems with externally forced switchings,” 2018 57th Annual Conference of the Society of Instrument and Control Engineers of Japan (SICE), pp. 1098-1103, 2018, doi: 10.23919/SICE.2018.8492568.
- S. Katayama, Y. Satoh, M. Doi and T. Ohtsuka, “Nonlinear model predictive control for systems with state-dependent switches and state jumps using a penalty function method,” 2018 IEEE Conference on Control Technology and Applications (CCTA), pp. 312-317, 2018, doi: 10.1109/CCTA.2018.8511448.
- S. Katayama, Y. Satoh, M. Doi and T. Ohtsuka, “Nonlinear model predictive control for systems with autonomous state jumps using a penalty function method,” 2017 11th Asian Control Conference (ASCC), pp. 2125-2130, 2017, doi: 10.1109/ASCC.2017.8287503.
Open Source Software
-
robotoc
This is a collection of the very efficient C++/Python optimal control problem solvers for multibody robotic systems with/without contacts, e.g., for robot manipulators and legged robots.



-
maafa
This is a PyTorch implementation of a reinforcement-learning-based data-driven MPC proposed by S. Gros and M. Zanon, which I personally call “MPC as a Function Approximator”, as introduced in the paper.


- autogenu-jupyter
This is a Jupyter-based C++ code generation tool for MPC with the continuous/GMRES-type algorithms. The major differences from the Maple-version are: 1) Jupyter-based code generation interface, 2) Fischer-Burumeister function for inequality constraints, 3) the multiple-shooting variants of the continuous/GMRE method (possibly faster than the original continuation/GMRES).